Harmonic Analysis and Signal Processing
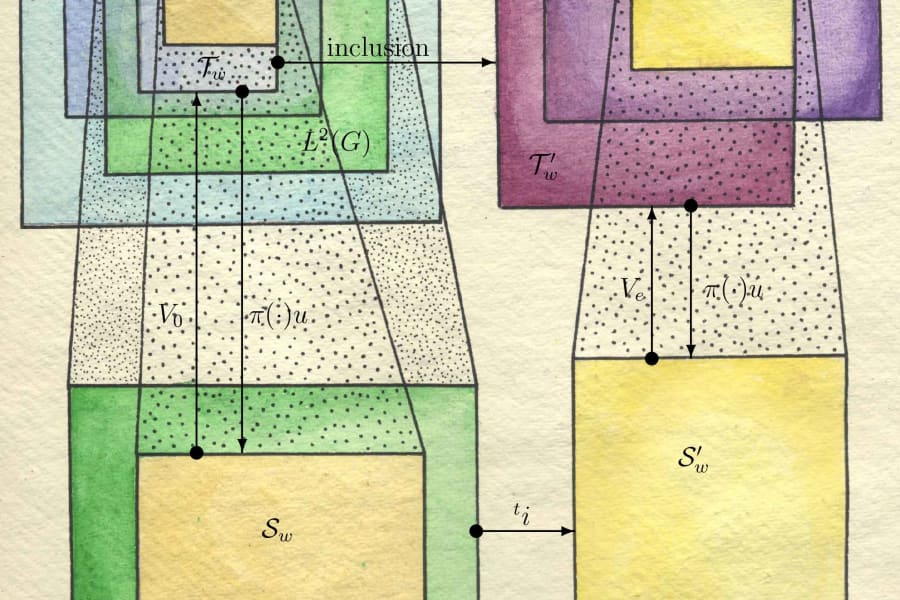
The research focus on frames that are defined in terms of square-integrable unitary representations of a locally compact group
CHarML
Our scientific interests focus on harmonic analysis, inverse problems, PDE and machine learning according to the following belief:
The analysis of massive, high-dimensional, noisy, time-varying data sets has become a critical issue for a large number of scientists and engineers. Major theoretical and algorithmic advances in analyzing massive and complex data are crucial, including methods of exploiting sparsity, clustering and classification, data mining, anomaly detection, and many more.
In the last decade we have witnessed significant advances in many individual core areas of data analysis, including machine learning, signal processing, statistics, optimization, and of course harmonic analysis. It appears highly likely that the next major breakthroughs will occur at the intersection of these disciplines (from Applied Harmonic Analysis, Massive Data Sets, Machine Learning, and Signal Processing).
Background image of the Needle tower by Kenneth Snelson at Kröller-Müller Museum
Research topics
Inverse Problems for PDEs
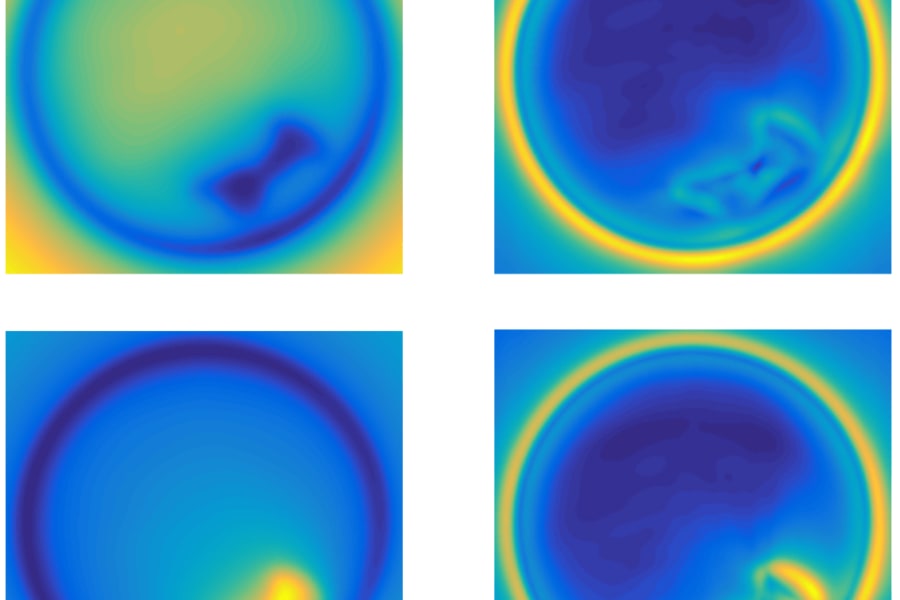
We are interested in inverse problems for elliptic and hyperbolic equations, including Calderon’s problem for electrical impedance tomography (EIT), photo-acoustic tomography (PAT), inverse scattering, Gel’fand-Calderon’s problem.
Mathematics of Machine Learning
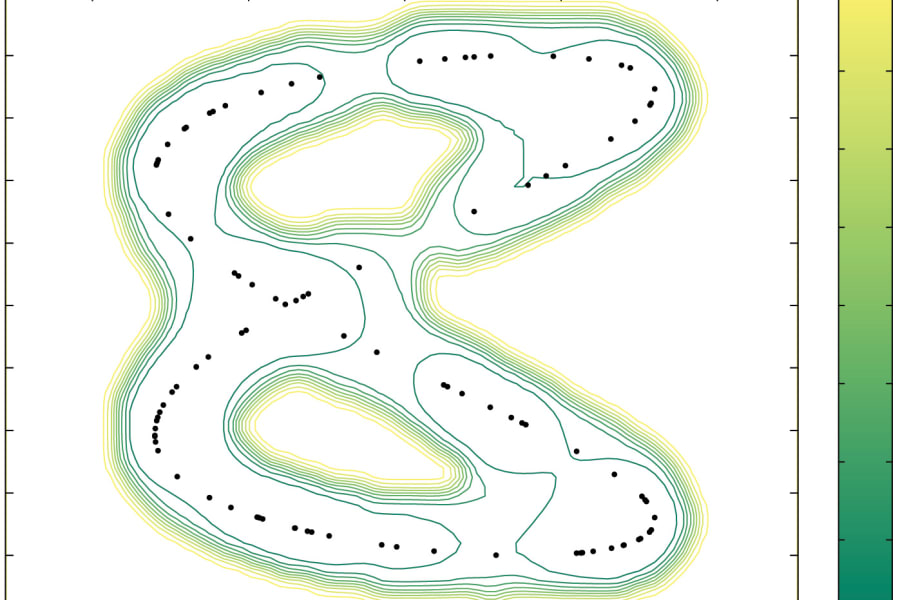
The activity is mainly devoted to show the interplay between learning theory and inverse problems.
People
Giovanni S.
AlbertiFilippo
De MariErnesto
De VitoMatteo
SantacesariaAlessandro
FelisiIşıl
GulekenPaolo
AngellaSimone
SannaMarkus
HolzleitnerWadim
GernerNesrine
ArouaFedor
Goncharov
Past People
People
Sara Farinelli | 2024 → 2025 | Post-doctoral fellow
Dennis Elbrächter | 2024 → 2025 | Post-doctoral fellow
Elena Rizzo | 2021 → 2024 | PhD student
Shiwei Sun | 2023 → 2024 | PhD student
Anupam Gumber | 2023 → 2024 | Post-doctoral fellow
Edgar Desainte-Maréville | 2024 | Student
Romain Petit | 2023 → 2024 | Post-doctoral fellow | Inverse Problems
Simone Sanna | 2023 | Student
Silvia Sciutto | 2020 → 2023 | PhD student | Inverse Problems
Lorenzo Sacchi | 2023 | Student
Luca Ratti | 2020 → 2023 | Post-doctoral fellow | Inverse Problems and Machine Learning
Simone Sanna | 2023 | Student | Compressed Sensing
Camilla Casaleggi | 2023 | Student
Camilla Casaleggi | 2022 | Student
Salvatore Ivan Trapasso | 2020 → 2022 | Post-doctoral fellow
Luca Wellmeier | 2022 | Student
Matteo Monti | 2019 → 2022 | PhD student | Harmonic Analysis
Stefano Vigogna | 2019 → 2021 | PhD student | Harmonic Analysis
Geraldo Macoj | 2021 | Student | Machine Learning
Beatrice Ravera | 2021 | Student | Analysis
Research projects
Most recent CHarML research projects
Sample complexity for inverse problems in PDE
Unit CHarMLLeading scientist Giovanni S. AlbertiRole within the project Principal InvestigatorDuration 2022 - 2027Sponsors EU | ERC StGTotal funding 1.15 M€- CLOSED
Compressed sensing for inverse problems in PDE
Unit CHarMLLeading scientist Giovanni S. AlbertiRole within the project Principal InvestigatorDuration 2021 - 2023Sponsors UniGeTotal funding 85 k€ - CLOSED
Machine Learning for Inverse Problems
Unit CHarMLLeading scientist Giovanni S. Alberti, Matteo SantacesariaRole within the project co-Principal InvestigatorDuration 2020 - 2023Sponsors AFOSRTotal funding 220 k€ - CLOSED
Infinite-dimensional inverse problems with finite measurements
Unit CHarMLLeading scientist Giovanni S. AlbertiRole within the project Principal InvestigatorDuration 2019 - 2021Sponsors UniGe Starting grantTotal funding 59.5 k€
Publications
Most recent CHarML publications
| Title | Year | Author | Venue |
|---|---|---|---|
| Market areas in general equilibrium | 2023 | Lanzara G.; Santacesaria M. | JOURNAL OF ECONOMIC THEORY |
| Short Communication: Localized Adversarial Artifacts for Compressed Sensing MRI | 2023 | Alaifari Rima; Alberti Giovanni S.; Gauksson Tandri | SIAM JOURNAL ON IMAGING SCIENCES |
| Inverse problems on low-dimensional manifolds | 2023 | Alberti G.; Arroyo A.; Santacesaria M. | NONLINEARITY |
| Neural networks for classification of strokes in electrical impedance tomography on a 3D head model | 2022 | Candiani V.; Santacesaria M. | MATHEMATICS IN ENGINEERING |
| Efficient Hyperparameter Tuning for Large Scale Kernel Ridge Regression | 2022 | Meanti Giacomo; Carratino Luigi; DE VITO Ernesto; Rosasco Lorenzo | INTERNATIONAL CONFERENCE ON ARTIFICIAL INTELLIGENCE AND STATISTICS, VOL 151 INTERNATIONAL CONFERENCE ON ARTIFICIAL INTELLIGENCE AND STATISTICS, VOL 151 |