Physics + learning + optimisation
We design and develop deep-learning image reconstruction methods inspired by physical modelling and optimisation schemes.
CIL
In our unit, we combine physical and mathematical modelling with optimisation and learning techniques to develop robust image reconstruction methods that perform effectively even under limited training data and potentially complex physical models. We focus particularly on modelling spatial distortions, non-Gaussian noise statistics, and the stochastic, time-dependent dynamics that arise in various fluorescence microscopy modalities. Our ultimate objective is to integrate these models into innovative reconstruction methods that fuse physics, optimization, and (deep) learning approaches.
Research topics
Self-adaptive algorithms
We develop algorithms for solving large-scale problems with minimal user dependence.
Breaking the diffraction barrier
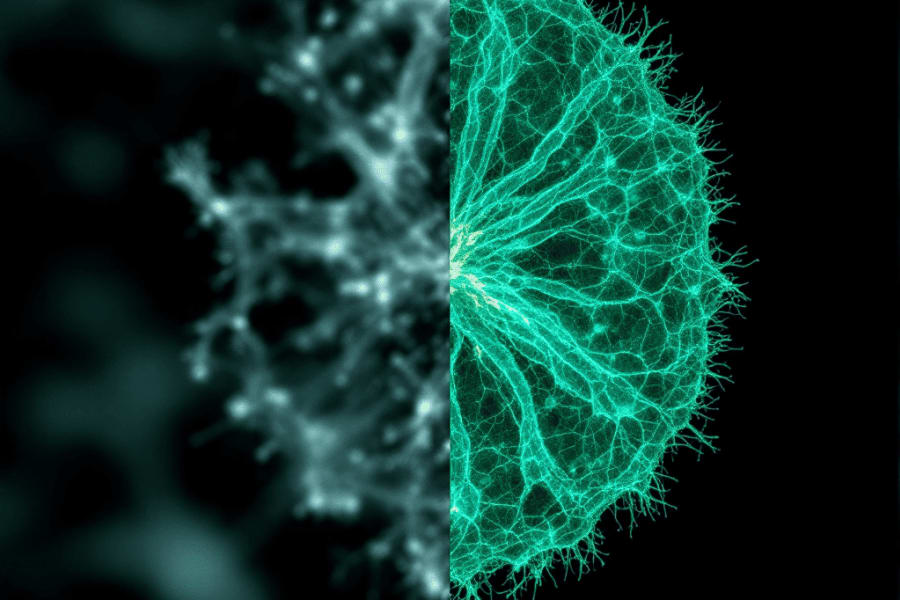
Our team aims at developing computational tools to overcome the resolution limit set by light diffraction in fluorescence microscopy.
Digital Humanities
Advanced digital image processing tools unveil the invisible in ancient paintings and illuminated manuscripts.
Computational imaging in action
Our computational approaches are applied to solve challenging problems arising in a plethora of applications ranging from medical imaging to computational neuroscience.
People
Luca
CalatroniNathan
BuskulicChristian
Daniele
Past People
People
Sofia Agostoni | 2025 | Research Scholar
Joseph Arnold | 2025 | Research Scholar
Publications
Most recent CIL publications
| Title | Year | Author | Venue |
|---|---|---|---|
| Say My Name: a Model’s Bias Discovery Framework | 2025 | C Fantasia L Calatroni X Descombes R Rekik | ArXiv Preprint |
| Box-constrained L0 Bregman-relaxations | 2025 | M Essafri L Calatroni E Soubies | ArXiv Preprint |
| Learning Spatially Adaptive l1-Norms Weights for Convolutional Synthesis Regularization | 2025 | A Kofler L Calatroni C Kolbitsch K Papafitsoros | ArXiv Preprint |
| Algorithmic unfolding for image reconstruction and localization problems in fluorescence microscopy | 2024 | S Bonettini L Calatroni D Pezzi M Prato | ArXiv Preprint |
| Exact continuous relaxations of l0-regularized criteria with non-quadratic data terms | 2024 | M Essafri L Calatroni E Soubies | HAL |